Tiefenwahrnehmung bei der Stereoprojektion
Gerhard P. Herbig, gph@herbig-3d.de1. Inhalt
Bei Stereoprojektionen kommt es immer wieder vor, dass einige Objekte in ihren Abmessungen ganz anders wahrgenommen werden, als man sie in Erinnerung hat. Einerseits kann dies ein durchaus erwünschter Effekt sein, beispielsweise dann, wenn ein nur 5cm großer Schmetterling so groß projiziert wird, als hätte er eine Flügelspannweite von 2m. Manchmal ist es aber auch störend - dann nämlich, wenn Menschen so aussehen, als wären sie nur einen Meter groß oder bei der Projektion Kugeln zu Eiern verzerrt werden. Dieser Artikel soll deshalb zwei zentrale Fragen beantworten:
1) Wann ist eine Stereo-Projektion formtreu?
2) Wann ist eine Stereo-Projektion form- und größentreu?
Wenn die Stereoprojektion ein formtreues Raumbild vermittelt, nennt man die Abbildung orthomorph (griechisch: "richtig in der Form"), und wenn die Abbildung form- und größentreu ist, tautomorph (griechisch: "identisch in der Form"). Innerhalb der Stereoskopie hat sich neben der Bezeichnung "orthomorph" auch der Begriff "orthostereoskopisch" durchgesetzt. Wir sprechen in diesem Fall dann von einer orthostereoskopischen Projektion oder einer orthostereoskopischen Abbildung.
Offensichtlich sind die Bedingungen für eine form- und größentreue (also tautostereoskopische) Projektion schärfer als die für eine nur formtreue (also orthostereoskopische).
Die folgenden Kapitel dieses Artikels sind folgendermaßen aufgebaut: In Kapitel 2 wird der Berechnungsgang genauestens erläutert und alle wichtigen geometrischen Größen eingeführt, mit denen dann in Kapitel 3 die virtuelle Größe, die virtuelle Breite und die virtuelle Tiefe eines projizierten Objektes berechnet werden können. Daraus werden dann in Kapitel 4 die Bedingungen für die form-, beziehungsweise form- und größentreue Projektion formuliert. Kapitel 5 diskutiert einige Fälle aus der Praxis, beispielsweise die Folgen einer Veränderung der Stereobasis, der Aufnahmebrennweite oder Einflüsse der Rahmung. Eine Zusammenfassung findet sich schließlich in Kapitel 6 und zum Schluss noch eine Liste aller verwendeten Formelzeichen.
2. Berechnungsablauf
Ziel der Berechnung ist es, herauszufinden, wie groß und wie tief uns ein Objekt bei der Stereoprojektion erscheint. Da dies eine subjektive Empfindung ist, wir aber vordringlich an objektiven Ergebnissen interessiert sind, benötigen wir einen Vergleich. Als Vergleichsgrundlage dient uns hierzu das natürliche Sehen und als Vergleichsgrößen dienen die auf die Netzhaut projizierten Bilder.
2.1 Bildhöhe, Deviation und Abstand
Jedes räumliche Objekt besitzt eine Höhe, eine Breite und eine Tiefe. Da sich die Höhe und die Breite bei allen Abbildungsvorgängen immer in gleicher Weise verändern, braucht nur einer von diesen beiden Werten berechnet werden. Für unsere Zwecke ist das Objekt also durch seine Größe und seine Tiefe vollständig beschrieben. Für die Bildhöhe des Netzhautbildes ist dann allein die Größe des Objektes maßgebend.
Die Information über die Tiefe eines Objektes geht bei einer einzelnen (Mono-) Abbildung verloren - erst im Stereobild ist (durch den Unterschied der beiden Stereohalbbilder) wieder Tiefeninformation vorhanden. Die Tiefeninformation über einen einzelnen Objektpunkt ist im horizontalen Versatz der zugehörigen korrespondierenden Bildpunkte enthalten. Somit erhält man einen ersten Hinweis über die Tiefenausdehnung eines Objektes durch die Differenz des maximalen und minimalen Bildpunkt-Versatzes. Diese Differenz wird Deviation genannt.
Die Deviation allein lässt allerdings noch keinen eindeutigen Rückschluss auf die Tiefenausdehnung eines Objektes zu. Erst im Zusammenhang mit der Entfernung, in der das Objekt wahrgenommen wird, ergibt sich für den Betrachter eine ganz bestimmte Wahrnehmung der Objekttiefe.
Bei jedem Abbildungsschritt müssen also diese drei Grundgrößen, die Bildhöhe h, die Deviation d und die Entfernung a berechnet werden. Mit Kenntnis dieser drei Größen ist die Wahrnehmung der Objektumrisse (Höhe, Breite und Tiefe) vollständig beschrieben.
2.2 Das natürliche Sehen
Ein erstes Gedankenexperiment: Wir betrachten aus der Entfernung a ein Objekt O mit der Größe g und der Tiefe t. Unsere Augen besitzen hierbei die Brennweite f0 und die Basis b0 . Die beiden auf der Netzhaut erzeugten Bilder sollen dann die Bildhöhe h0 und die Deviation d0 besitzen (die Berechnung dieser Größen erfolgt erst im nächsten Kapitel). Infolge der Konvergenzstellung unserer Augen (und unserer Gedächtnisleistung) nehmen wir das Objekt im Abstand a0 wahr. Der Index 0 steht hier und im folgenden immer für die Referenzsituation des natürlichen Sehens. Selbstverständlich gehen wir von einem funktionierenden Sehapparat aus, so dass a0 = a gelten soll. (Wir nehmen das Objekt dort war, wo es tatsächlich auch ist.)
2.3 Aufnahme und Projektion
Ein weiteres Gedankenexperiment: Wir nehmen das gleiche Objekt O mit einer Stereokamera auf, projizieren das Bild auf eine Leinwand und betrachten nun die Stereoprojektion. Die Höhe des Netzhautbildes sei jetzt hv , die Deviation dv und die Entfernung, in der wir das Objekt wahrnehmen, av (der Index v steht für die Betrachtung des virtuellen Bildes auf der Leinwand). Schließlich sind gv die virtuelle Größe und tv die virtuellen Tiefe, mit der wir das Objekt wahrnehmen.
2.4 Die form- und größentreue Projektion
Offensichtlich nehmen wir das Objekt genau dann mit unverfälschten äußeren Abmessungen wahr, wenn folgende Bedingungen erfüllt sind (virtuelle Werte sind identisch mit den echten Werten):
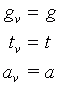 . (2.1)
. (2.1)
Diese Gleichung (2.1) ist schon eine erste sehr allgemeine Definition für die form- und größentreue Projektion. Später werden wir daraus noch eine Menge Details ableiten.
Die Bedingung für eine form- und größentreue Abbildung konnten wir noch relativ leicht aufschreiben. Wann jedoch ist eine Abbildung nur formtreu? Bei beliebig gewählten Aufnahme- und Wiedergabeparametern werden wir Gleichungen der Form:
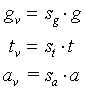 (2.2)
(2.2)
erhalten. Die hier neu eingeführten Koeffizienten sg , st und sa seien die Abbildungskoeffizienten für die Entfernung, die Größe und die Tiefe. Damit ergibt sich eine formtreue Abbildung für
wenn also die Abbildungskoeffizienten für die Größe und die Tiefe identisch sind. Über die Entfernung wird an dieser Stelle noch keine Aussage gemacht.
3. Berechnungsdurchführung
In diesem Kapitel soll nun die eigentliche Durchführung der Berechnung erfolgen. Wieder soll zu Beginn die Referenzsituation des natürlichen Sehens stehen:
3.1 Die Abbildung im Auge beim natürlichen Sehen
Wir betrachten zunächst das Bild 1, obere Hälfte. Ein Objekt mit der Größe g wird aus dem Abstand a betrachtet. Der Abstand der Augenlinse zur Netzhaut sei näherungsweise gleich der Brennweite der Augenlinse, also gleich fo . Dann erhalten wir für die uns interessierende Höhe des Netzhautbildes h0 sofort:
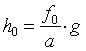 . (3.1)
. (3.1)
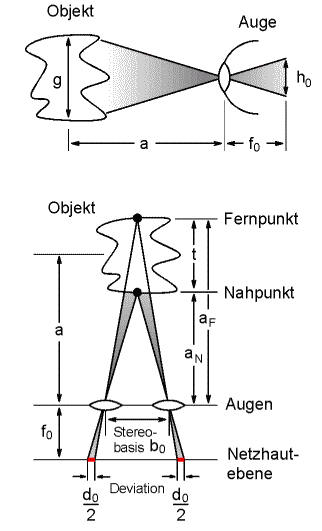 |
| Bild 1: Die Abbildung im Auge beim natürlichen Sehen. Oben: Höhenabbildung, unten: Tiefenabbildung. |
Entsprechend erhalten wir aus der unteren Hälfte von Bild 1 ebenfalls mit Hilfe des Strahlensatzes (zweimal den Strahlensatz ansetzen, einmal für den Fernpunkt, einmal für den Nahpunkt, dann die Deviation als Differenz der Bildpunkte des Nahpunktes und der Bildpunkte des Fernpunktes berechnen):
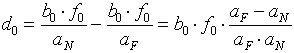 . (3.2)
. (3.2)
Hier ist d0 die zu berechnende Deviation und b0 der Abstand der beiden Augen. Im Nenner können wir die Differenz aus Fernpunktweite aF und Nahpunktweite aN direkt durch die Stereotiefe t ersetzen:
und im Zähler verwenden wir für den Objektabstand das geometrische Mittel aus Fern- und Nahpunktweite:
Beides oben eingesetzt ergibt schließlich:
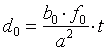 . (3.5)
. (3.5)
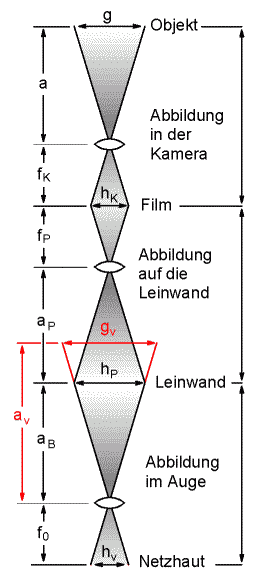
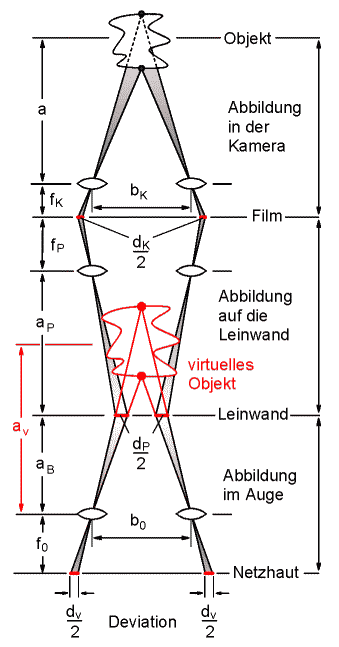
Die Gleichungen (3.1) und (3.5) sind im folgenden die Vergleichsgrundlagen für die Objektwahrnehmung bei der Stereoprojektion, die man in eine Kameraabbildung, eine Projektion auf die Leinwand und eine Betrachtung des Projektionsbildes unterteilen kann. Diese drei Teilabbildungen sind als Kettenabbildung in Bild 2 und Bild 3 skizziert, und zwar in Bild 2 die Höhenabbildung und in Bild 3 die Tiefenabbildung:
 |
 |
|
| Bild 2: Höhenabbildung als Kettenabbildung der Kameraabbildung, der Abbildung auf die Leinwand und der Abbildung im Auge. |
Bild 3: Tiefenabbildung als Kettenabbildung der Kameraabbildung, der Abbildung auf die Leinwand und der Abbildung im Auge. |
3.2 Die Abbildung in der Kamera
Die Bilder 2 und 3 - jeweils oberes Drittel - zeigen die Abbildung in der Kamera. Formal erhalten wir genau die gleichen Formeln wie beim natürlichen Sehen (Gleichung (3.1) und (3.5)), jetzt aber mit der Aufnahmebrennweite fK , der Bildhöhe hK , und der Stereobasis bK . Die Deviation, die wir bei der Aufnahme erhalten, ist dK :
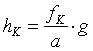 , (3.6)
, (3.6)
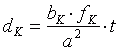 . (3.7)
. (3.7)
3.3 Die Abbildung auf der Leinwand
Das Dia wird bei der Projektion linear auf die Leinwand vergrößert. Der Projektor habe hierbei die Brennweite fP und stehe im Abstand aP von der Leinwand entfernt. Die Bildhöhe und die Deviation werden mit dem gleichen Vergrößerungsfaktor V = aP / fP auf die Leinwand projiziert, siehe dazu Bild 2 und Bild 3 - jeweils mittleres Bilddrittel. Die Bildhöhe auf der Leinwand hP und die Deviation auf der Leinwand dP sind deshalb:
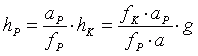 , (3.8)
, (3.8)
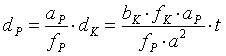 . (3.9)
. (3.9)
3.4 Die Abbildung im Auge bei der Stereoprojektion
Der letzte Schritt ist nun die Abbildung des Leinwandbildes auf die Netzhaut des Betrachters. Auch dies ist eine lineare Abbildung mit identischem Vergrößerungsfaktor für Bildhöhe und Deviation. Der Betrachter stehe im Abstand aB vor der Leinwand und seine Augenlinsen haben wieder die Brennweite f0 . Die virtuelle Bildhöhe und die virtuelle Deviation des Netzhautbildes seien jetzt hv und dv . Diese Abbildungen sind ebenfalls in Bild 2 und Bild 3 - jeweils unteres Bilddrittel - aufgezeichnet:
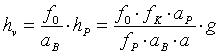 , (3.10)
, (3.10)
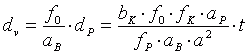 . (3.11)
. (3.11)
3.5 Der virtuelle Abstand
Eine besondere Rolle spielt der Abstand, in dem wir ein Objekt bei der Stereoprojektion wahrnehmen. Dieser Abstand ist der virtuelle Abstand av . Er ist ebenfalls in Bild 3 (rot) eingezeichnet. Wir sehen, dass wir dort das Objekt hinter der Leinwand wahrnehmen. Um den virtuellen Abstand genauer herzuleiten, werden noch weitere Größen benötigt, die in Bild 4 eingezeichnet sind.
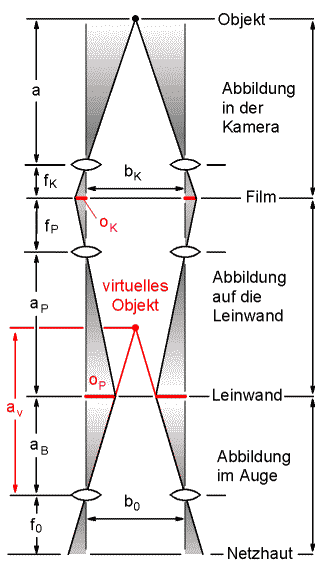 |
| Bild 4: Zur Berechnung des virtuellen Abstandes eines punktförmigen Objektes bei der Stereoprojektion. |
Der Bildpunkt eines punktförmigen Objektes besitzt in der Filmebene gegenüber dem Unendlichpunkt einen seitlichen Versatz. Dieser Versatz wird parallaktische Verschiebung oK (K für Kamera) genannt:
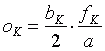 . (3.12)
. (3.12)
Diese parallaktische Verschiebung wird mit dem Vergrößerungsfaktor V = aP /fP auf die Leinwand abgebildet. Dort ist also der Versatz oP :
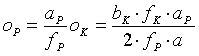 . (3.13)
. (3.13)
Mit gegebenem oP ist schließlich auch der virtuelle Abstand berechenbar:
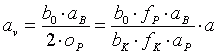 . (3.14)
. (3.14)
3.6. Virtuelle Größe und virtuelle Tiefe
Bisher haben wir aus rein geometrischen Überlegungen lediglich Aussagen über das Netzhautbild erhalten (hv und dv). Der entscheidende Schritt, nämlich der Schluss auf die virtuellen Wahrnehmungsgrößen gv und tv erfolgt erst jetzt: Ausgehend von (3.1) und (3.5) definieren wir die virtuelle Objektgröße gv über die virtuelle Bildhöhe:
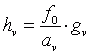 , (3.15)
, (3.15)
und die virtuelle Objekttiefe tv über die virtuelle Deviation:
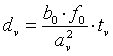 . (3.16)
. (3.16)
In beiden Fällen muss natürlich der virtuelle Abstand av berücksichtigt werden.
Durch Vergleich von (3.10) mit (3.15) und (3.11) mit (3.16) erhält man schließlich für die virtuellen Objektwerte (und jeweils nach Elimination von av mit Gleichung (3.14)):
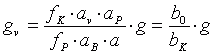 , (3.17)
, (3.17)
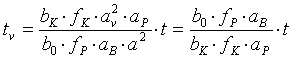 . (3.18)
. (3.18)
An dieser Stelle führen wir noch eine Abkürzung ein und nennen diese den Tiefenfaktor T :
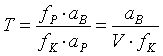 . (3.19)
. (3.19)
Mit dieser Abkürzung formulieren wir nochmals die Gleichungen (3.14), (3.17) und (3.18):
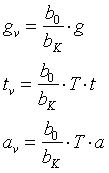 (3.20)
(3.20)
und vergleichen dieses Ergebnis mit (2.2). Damit haben wir eine sehr kompakte Formulierung für die Abbildungskoeffizienten gefunden:
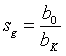 (3.21)
(3.21)
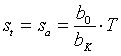 . (3.22)
. (3.22)
4. Ortho- und Tautostereoskopie
Mit den Vorleistungen aus Kapitel 3 können wir nun sehr einfach die eingangs gestellten Fragen, wann eine form- und größentreue, und wann eine nur formtreue Abbildung vorliegt, beantworten.
4.1 Die tautostereoskopische (form- und größentreue) Abbildung
Eine form- und größentreue Abbildung ist genau dann gegeben, wenn sg = st = sa = 1 gilt, oder
und gleichzeitig
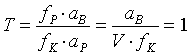 (4.2)
(4.2)
erfüllt sind. Zur tautostereoskopischen Abbildung sind also genau zwei Voraussetzungen notwendig: Erstens muss die Aufnahmebasis bK genauso groß sein wie der Augenabstand b0 (Gleichung (4.1)) und zweitens müssen die Brennweiten der Aufnahmekamera und des Stereoprojektors sowie die Entfernungen des Projektors und des Betrachters zur Leinwand in einem bestimmten Verhältnis stehen (Gleichung (4.2)). Da die einzige Möglichkeit, bei einer Projektion den Tiefenfaktor T nachträglich zu beeinflussen, darin besteht, den Betrachtungsabstand aB zur Leinwand zu verändern (an den drei anderen Parametern lässt sich während der Projektion in der Regel nichts mehr ändern), kann man im Projektionssaal einen besonderen Punkt
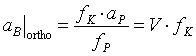 (4.3)
(4.3)
definieren, von dem aus für den Betrachter eine form- und größentreue Darbietung möglich ist, solange Gleichung (4.1) ebenso erfüllt ist. Weil von diesem Betrachtungspunkt das Raumbild immer formtreu (orthostereoskopisch) wirkt, wird dieser Punkt auch orthostereoskopischer Punkt genannt.
4.2 Die orthostereoskopische (nur formtreue) Abbildung
Die Bedingung für eine formtreue Abbildung wurde schon in Gleichung (2.3) formuliert. Mit (3.20) erhält man daraus:
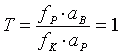 , (4.4)
, (4.4)
also das gleiche Ergebnis wie zuvor, jetzt aber ohne die Bedingung für die Stereobasis. Bei einer Betrachtung vom orthostereoskopischen Punkt ist die Formtreue also immer erfüllt. Besonders interessant erscheint die Tatsache, dass die Formtreue allein durch die Einhaltung von (4.4) erreicht werden kann - bei beliebiger Stereobasis. Variiert man umgekehrt nur die Stereobasis, hat dies ausschließlich eine Wirkung auf den Größeneindruck - eine Formveränderung findet durch Veränderung der Stereobasis also nicht statt! Dieses Ergebnis mag im ersten Moment überraschen - und möglicherweise auch im Widerspruch zu eigenen Erfahrungen stehen, stellt man doch gerade bei Makro- oder Großbasisaufnahmen am häufigsten Tiefenverzerrungen fest. Das liegt aber nicht an der veränderten Stereobasis, sondern in der Regel an der Rahmung der Stereodias. Bevor wir nun im nächsten Kapitel noch genauer auf die Rahmung eingehen werden, wollen wir den Tiefenfaktor T noch etwas genauer betrachten.
Angenommen, der Tiefenfaktor T sei größer als 1, beispielsweise infolge eines größeren Betrachtungsabstandes aB , als es Gleichung (4.3) vorschreibt (der Betrachter befindet sich also im Projektionssaal hinter dem orthostereoskopische Punkt), dann nimmt nach (3.20) auch die virtuelle Tiefe tv linear mit T zu, nicht aber die virtuelle Größe gv . Dies bedeutet, dass uns die Objekte tiefer erscheinen, wenn wir uns weiter hinten im Saal befinden, und flacher, wenn wir weiter vorne sitzen. Dieser Effekt läßt sich auch folgendermaßen erklären:
Wenn wir uns beim natürlichen Sehen von einem Objekt entfernen, nimmt die Bildgröße h0 auf der Netzhaut nur linear mit der Entfernung ab, die Deviation d0 aber quadratisch (Gleichungen (3.1) und (3.5)). Diese Abhängigkeiten sind fest in unserem Gehirn programmiert und bei jeder Abweichung davon meldet unser Gehirn eine Formverzerrung. Entfernen wir uns nun bei der Stereoprojektion von der Leinwand, nehmen sowohl die virtuelle Bildgröße hv als auch die virtuelle Deviation dv nur linear ab (Gleichungen (3.10) und (3.11), im Nenner jeweils aB). Der Wert für die Deviation ist also in diesem Beispiel zu groß (verglichen mit der Entfernung von einem natürlichen Objekt) und damit erscheint uns das Objekt zu tief.
Noch eine andere Interpretation lässt Gleichung (3.20) zu: Offensichtlich ist genau dann eine formtreue Bildwahrnehmung garantiert (also T = 1), wenn wir das Bild im virtuellen Abstand
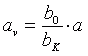 (4.5)
(4.5)
wahrnehmen. Schon jetzt sehen wir, dass diese Forderung in der Praxis kaum einzuhalten ist. Angenommen, wir porträtieren mit einer normalen Stereokamera eine Person aus 2 m Entfernung, dann ist eine formtreue Wahrnehmung nur möglich, wenn wir bei der Projektion das virtuelle Bild dieser Person ebenfalls in einer Entfernung von 2m orten. Diese Forderung kann allenfalls noch im eigenen Wohnzimmer erfüllt werden, mit Sicherheit aber nicht mehr bei einer Saalprojektion (Ausnahme: IMAX 3D). Ähnliche Schwierigkeiten treten bei Makroaufnahmen auf, die nicht selten aus sehr geringen Entfernungen angefertigt werden. Auch die deutliche Reduktion der Stereobasis gegenüber dem Augenabstand vermag die geforderte virtuelle Entfernung nicht mehr auf ein realistisches Maß vergrößern zu können (Beispiel: Aufnahmeabstand = 30cm und Stereobasis = 1cm ergibt bei angenommenen 6,5cm Augenabstand nach Gleichung (4.5) einen geforderten virtuellen Abstand von ebenfalls etwa 2m).
Der virtuelle Größeneindruck ist übrigens genau umgekehrt proportional zur Stereobasis. Nach (3.20) erscheint uns bei halbierter Stereobasis ein projiziertes Objekt genau doppelt so groß wie in Wirklichkeit - und bei verdoppelter Stereobasis nur noch halb so groß. Diesen Effekt wird jeder leicht nachvollziehen können, der schon einmal Makro- oder Großbasis-Stereodias projiziert hat.
5. Einflüsse der Diarahmung
Bei allen bisherigen Gleichungen spielte die Rahmung der Stereodias überhaupt noch keine Rolle. Selbstverständlich müssen wir aber zur Projektion in Kapitel 3.4 und 3.5 die Stereodias in irgendeiner Form gerahmt haben. Tatsächlich haben wir dort auch unterstellt, dass die beiden korrespondierenden Unendlich-Punkte im Augenabstand auf die Leinwand projiziert werden (siehe auch Bild 3 und Bild 4). Diese sogenannte natürlich Projektion erlaubt nicht nur eine form- beziehungsweise form- und größentreue Projektion, sie garantiert auch divergenzfreie Augenachsen für jeden Betrachter, unabhängig vom Bildinhalt oder von der Betrachtungsentfernung von der Leinwand. (Der Abstand der Unendlich-Punkte auf der Leinwand ist neben der Rahmung auch von der Ausrichtung der Projektoren abhängig. Für die Auswirkungen auf die Raumwahrnehmung ist allerdings nur das Gesamtergebnis, also die Lage der Bilder auf der Leinwand relevant. Ich habe deshalb für die oben beschriebene Situation die Bezeichnung natürliche Projektion gewählt.)
Wir werden nun Gleichung (3.20) nochmals neu formulieren, jetzt aber mit beliebiger Lage der Stereodias in den Diarähmchen. Wir nehmen im folgenden an, dass der Abstand der beiden Dias gegenüber der Position der natürlichen Projektion um den Wert r verringert worden sei. Hierbei ist es gleichgültig, ob das linke oder das rechte Dia aus seiner ursprünglichen Position verschoben wurde. Bei dieser Manipulation ändert sich der virtuelle Abstand av nach Gleichung (3.14). Wir müssen diesen also neu formulieren, wobei wir im ersten Schritt anstatt oK jetzt
schreiben, da sich die parallaktische Verschiebung des zu betrachtenden Raumpunktes ebenfalls um den Wert r ändert. Entsprechend gilt für die parallaktische Verschiebung auf der Leinwand:
Als Ersatz von (3.14) gilt also für den virtuellen Abstand:
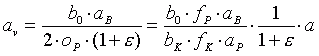 . (5.3)
. (5.3)
Wir schreiben in Erweiterung zu (3.20):
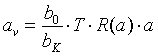 (5.4)
(5.4)
und haben hierbei den Rahmungsfaktor R eingeführt:
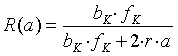 . (5.5)
. (5.5)
Dieser Rahmungsfaktor ist neben der Kamerabasis bK und der Kamerabrennweite fK leider auch noch von der Objektentfernung a abhängig, d.h., für jedes abgebildete Objekt ergibt sich bei konstanter Verschiebung r ein anderer Rahmungsfaktor.
Im nächsten Schritt wiederholen wir die Berechnung aus Kapitel 3.6 und lösen (3.15) und (3.16) nach gv und tv auf, verwenden aber jetzt nicht den virtuellen Abstand nach (3.14), sondern nach (5.4).
Damit erhalten wir anstelle von (3.20):
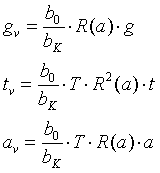 . (5.6)
. (5.6)
Diese Gleichung (5.6) muss Gleichung (3.20) natürlich für den Sonderfall R(a) = 1 enthalten. Der Rahmungsfaktor R geht in die drei virtuellen Werte Größe, Tiefe und Entfernung leider unterschiedlich ein. Die virtuelle Größe und die virtuelle Entfernung steigen linear mit R, die virtuelle Tiefe aber quadratisch. Bei positivem r, also Verringerung des Diaabstandes, ist R < 1. Die Tiefenausdehnung nimmt damit stärker ab als die Größe und das virtuelle Objekt erscheint uns näher und kleiner, aber eben auch flacher.
Zusätzlich ist zu berücksichtigen, dass R(a) nicht konstant ist, sondern ebenfalls noch von der Objektentfernung a abhängt, siehe Gleichung (5.5).
Eine formtreue Änderung hätte sich nur ergeben, wenn R(a) in allen drei Größen einen gleichen und von a unabhängigen Einfluss gehabt hätte. So aber ist jede Abweichung von der natürlichen Projektion mit einer Tiefenverzerrung verbunden.
Allerdings ist es möglich, für räumlich begrenzte Objekte eine punktuelle Formtreue zu definieren, bei der ein Objekt nur in der Mitte tatsächlich formtreu erscheint. Wir erreichen genau diese Situation, wenn wir für die Objektmitte aM (entweder durch Wahl eines geeigneten Betrachtungsstandortes oder durch eine entsprechende Diarahmung) die Bedingung
erfüllen. Damit lässt sich in Gleichung (5.6) der Tiefenfaktor T eliminieren:
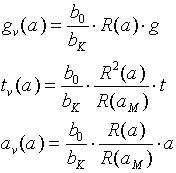 . (5.8)
. (5.8)
Die zusätzlichen Abhängigkeiten von a bewirken, dass die vorderen Objektelemente zu flach und die hinteren Objektelemente zu tief erscheinen. Im Bereich der Objektmitte gilt näherungsweise a » aM und deshalb:
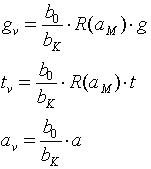 . (5.9)
. (5.9)
Wir sehen das Objekt also zusätzlich in der Größe mit dem Faktor R(aM) (b0 / bK) skaliert, aber näherungsweise formtreu.
Da ein Betrachtungsabstand aB , der die Bedingung (5.7) erfüllt, offensichtlich auch in diesen Fall eine halbwegs formtreue Betrachtung ermöglicht, wollen wir diesen Abstand den quasi-orthostereoskopischen Punkt nennen:
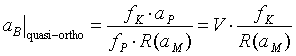 . (5.10)
. (5.10)
Von diesem Punkt aus nehmen wir das Objekt im (b0 / bK) - fachen Abstand wahr und es erscheint uns in der Größe um den Faktor R(aM) (b0 / bK) skaliert. Leider ist dieser quasi-orthostereoskopische Punkt von der Objektentfernung abhängig und kann deshalb auch nur für ein einzelnes isoliertes Objekt angegeben werden.
Um Gleichung (5.7) zu erfüllen ist die Verschiebung r entsprechend
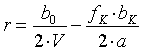 . (5.11)
. (5.11)
zu wählen (Gleichung (5.7) mit (5.10) und (3.19)).
Übrigens ist es für die hier getroffenen Aussagen völlig unerheblich, ob das Dia im Rahmen um die Strecke r, oder das Projektionsbild auf der Leinwand um Vr verschoben wird. Dies hat lediglich einen Einfluss auf das Scheinfenster, nicht jedoch auf die hier interessierende Tiefenverzerrung der abgebildeten Objekte.
5.1 Stereo-Makrofotografie
In der Stereo-Makrofotografie wird häufig ein räumlich allseitig begrenztes Objekt aufgenommen und das Stereobild anschließend so gerahmt, dass es in der Leinwandebene zu sehen ist. Welche Aufnahmebasis ist zu wählen, um dieses Objekt dann im quasi-orthostereoskopischen Sinne auch formtreu wahrnehmen zu können? Die Antwort auf diese Frage gibt Gleichung (5.9/3) mit av = aB :
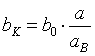 . (5.12)
. (5.12)
In der Praxis wird die Stereobasis jedoch häufig etwas größer gewählt, um dem Raumbild - auf Kosten der Formtreue - eine größere Tiefenausdehnung zu geben.
Beispiel: Angenommen wir fotografieren eine Blüte mit den Aufnahmeparametern Abstand a = 300 mm, Brennweite fK = 100 mm und Stereobasis bK = 15mm. Bei einer Projektion sei die Projektionsvergrößerung V = 60 (ergibt ein etwa 2m breites Bild bei 35mm Film) und der Abstand des Betrachters mit der Augenbasis b0 = 60mm von der Leinwand sei aB = 4m. Die Gleichungen (3.19) und (3.20) ergeben bei natürlicher Projektion einen Tiefenfaktor:
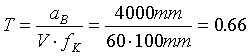 , (5.13)
, (5.13)
und damit
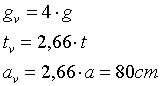 . (5.14)
. (5.14)
Das Objekt erscheint dem Betrachter also in einem virtuellen Abstand von 80cm und dabei gestaucht in der Tiefe um den Faktor 0,66 (der orthostereoskopische Abstand nach Gleichung (4.3) liegt in einer Entfernung von 6m von der Leinwand).
Nun wird der Abstand der Dias im Diarahmen etwas vergrößert, um den virtuellen Objektabstand zu erhöhen (und die Blüte in die Leinwandebene zu ziehen). Verfolgen wir einmal, was passiert, wenn der Abstand der Dias im Diarahmen um r = -2mm vergrößert wird. Wir berechnen dazu den Rahmungsfaktor R nach Gleichung (5.5):
 (5.15)
(5.15)
und erhalten die virtuellen Größen wieder nach Gleichung (5.6):
 . (5.16)
. (5.16)
Wir haben also durch die Rahmung erreicht, dass das Objekt nun in der Leinwandebene gesehen wird (av = 4m), jedoch um den Preis einer entsetzlich übertriebenen Tiefe (um den Faktor st / sg = 66,66 / 20 = 3,33). Wählen wir jedoch die Aufnahmebasis nach (5.12):
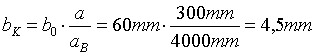 , (5.17)
, (5.17)
sehen wir das Objekt in der Leinwandebene quasi-orthostereoskopisch (sg = st = 20).
6. Zusammenfassung
Eine formtreue (orthostereoskopische) Abbildung erhält man nur, wenn zwei Voraussetzungen erfüllt sind:
1) Es liegt eine natürliche Projektion vor, das heißt, die korrespondierenden Unendlich-Punkte werden im Augenabstand auf die Leinwand projiziert.
2) Die Betrachtung des Projektionsbildes erfolgt vom orthostereoskopischen Punkt nach Gleichung (4.3).
Wird zusätzlich verlangt, dass die Abbildung auch größentreu (tautostereoskopisch) sein soll, muss die Aufnahmebasis der Kamera dem Augenabstand entsprechen, siehe Gleichung (4.1).
Die Betrachtung ist immer dann formtreu, wenn das virtuelle Objekt im Aufnahmeabstand, skaliert mit dem Verhältnis des Augenabstandes zur Aufnahmebasis, wahrgenommen wird, siehe Gleichung (4.5).
Falls keine natürliche Projektion vorliegt, ist eine formtreue Abbildung nicht mehr möglich. Vom quasi-orthostereoskopischen Betrachtungspunkt nach Gleichung (5.10) wird streng genommen nur noch die Objektmitte formtreu wahrgenommen, die vorderen Objektelemente erscheinen zu flach und die hinteren Objektelemente zu tief.
Liste der verwendeten Symbole:
a : Entfernung zum Objekt, sowohl beim natürlichen Sehen als auch bei der Aufnahme
aB : Abstand des Betrachters von der Leinwand
aN : Nahpunktweite, die Entfernung vom Betrachter zum nächstliegenden Objektpunkt
aF : Fernpunktweite, die Entfernung vom Betrachter zum entferntesten Objektpunkt
aM : Entfernung zur Objektmitte
aP : Abstand des Projektors von der Leinwand
av virtuelle Entfernung, in der man das Objekt bei der Stereoprojektion wahrnimmt
b0 : Augenabstand des Betrachters
bK : Stereobasis der Aufnahmekamera
d : Deviation, Differenz zwischen dem maximalen und dem minimalen Bildpunktversatz eines Objektpunktes in einem Stereobild
dK : Deviation im Diapositiv
dP : Deviation auf der Leinwand
dv : Deviation des virtuellen Bildes auf der Netzhaut
f0 : Brennweite der Augenlinsen
fK : Brennweite der Kamera
fP : Brennweite des Projektors
g : Objektgröße
gv : virtuelle Objektgröße bei der Stereoprojektion
h : Objekthöhe
h0 : Höhe des Objektbildes beim natürlichen Sehen auf der Netzhaut
hK : Höhe des Objektbildes auf dem Diapositiv
hP : Höhe des Objektbildes auf der Leinwand
hv : Höhe des Objektbildes auf der Netzhaut bei der Stereoprojektion
oK : parallaktische Verschiebung des Bildpunktes auf dem Diapositiv relativ zum Unendlichpunkt
oP : parallaktische Verschiebung auf der Leinwand relativ zum Unendlichpunkt
r : Seitlicher Rahmungsversatz des Diapositives
R : Rahmungsfaktor
sa : Skalierungsfaktor Objektentfernung
sg : Skalierungsfaktor Objektgröße
st : Skalierungsfaktor Objekttiefe
t : Objekttiefe
tv : virtuelle Objekttiefe bei der Stereoprojektion
T : Tiefenfaktor
V : Vergrößerungsfaktor bei der Projektion
Dieser Artikel steht im Downloadbereich auch zum Herunterladen als pdf-Dokument bereit.