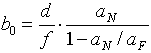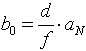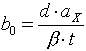Anmerkungen zur Stereofotografie mit
verkleinerter oder vergrößerter Basis
Gerhard P. Herbig,
gph@herbig-3d.de
Gegenüber dem natürlichen Sehen mit dem Augenabstand als Stereobasis ermöglicht die Stereofotografie mit einer verkleinerten oder vergrößerten Aufnahmebasis eine eindrucksvolle Erweiterung des räumlichen Wahrnehmungsbereiches. Der Betrachter dringt so in Bereiche vor, die ihm ansonsten auf Grund seines unveränderlichen Augenabstandes verwehrt bleiben. Dies macht diese spezielle Art der Fotografie zu einem äußerst reizvollen Betätigungsfeld. Die zu beachtenden Regeln und Abhängigkeiten sind bei Aufnahmen mit gegenüber dem Augenabstand vergrößerter bzw. verkleinerter Basis unterschiedlich und werden deshalb in den folgenden Abschnitten getrennt behandelt.
1. Aufnahmen mit vergrößerter Stereobasis
1.1 Technik. Benötigt werden zwei synchron auslösbare Monokameras, wobei höchste Präzision nur mit elektrischer Auslösung erreicht werden kann. Um Fertigungstoleranzen der Kameras auszugleichen, sollte zur Justierung der Auslösezeitpunkte das Auslösesignal der schnelleren Kamera um den Differenzbetrag elektrisch verzögert werden. Zur Not lassen sich die Kameras auch pneumatisch koppeln, eine für viele Anwendungen vollkommen ausreichende und darüber hinaus auch sehr zuverlässige Methode. Stilleben können grundsätzlich auch sequentiell fotografiert werden, jedoch sind die Empfindlichkeiten gegenüber geringsten Veränderungen zwischen den beiden Aufnahmen extrem hoch. Problematisch sind erfahrungsgemäß vorüberziehende Wolken, sich (auch bei leichtem Wind) bewegende Blätter sowie Reflektionen an Wasseroberflächen.
1.2 Liliputismus. Bei vergrößerter Aufnahmebasis erscheinen alle Objekte perspektivisch verkleinert, ähnlich wie in einer Modell-Landschaft. Diesen Effekt nennt man Liliputismus; er ist eine zwangsläufige Folge des Gewinns an räumlicher Tiefenwahrnehmung.
1.3 Aufnahmegeometrie. Geometrische Verzeichnungen der Aufnahme führen in jedem Fall zu einer Betrachtungsstörung, meistens aber jedoch zu einem unbrauchbaren Ergebnis. Da solche Verzeichnungen nachträglich nicht mehr korrigiert werden können, müssen
- die Aufnahmerichtungen für das linke und das rechte Stereobild parallel,
- die Aufnahmerichtungen lotrecht zur Basislinie und
- die Basislinie selbst waagerecht ausgerichtet werden.
1.4 Berechnung der Aufnahmebasis.
Immer wieder taucht die Frage nach der optimalen
Stereobasis auf, die es natürlich nicht geben kann, denn
die von ihr abhängige räumliche Tiefenwahrnehmung
ist eine nicht meßbare physiologische Größe.
Meßbar ist lediglich die Deviation
d, die maximale in einem Stereobild enthaltene
horizontale Verschiebung zweier korrespondierender Bildpunkte
(siehe Bild 1). Die Deviation ist zwar kein objektives
Maß für die Tiefenwirkung, aber sie liefert
immerhin einen Anhaltspunkt für die Wahl einer
geeigneten Aufnahmebasis, um Stereofotos mit angemessener
Tiefeninformation zu erhalten. In der Kleinbildfotografie
akzeptiert man für die Deviation im allgemeinen einen
Grenzwert von d = 1,2mm [1].
 |
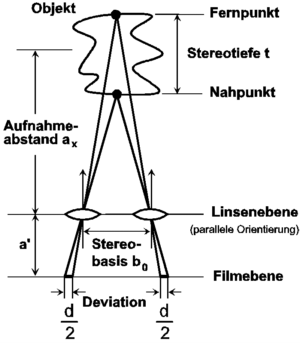| Bild 1: Die Aufnahmesituation. |
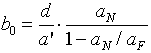. (1)
Hierbei bedeuten:
b0 : Stereobasis, d : Deviation,
a' : Abstand Filmebene zur Hauptebene,
aN : Nahpunktweite und
aF : Fernpunktweite.
Solange die verwendete Aufnahmebasis gleich groß oder größer ist als der Augenabstand, läßt sich von dieser Vorschrift folgende praxisgerechte Näherung ableiten, die auch von der Stereo-Rechenscheibe für 'Normal- und Fernaufnahmen' verwendet wird:
. (2)
Zusätzlich ist jetzt: f : Brennweite. In dieser Näherung wird a' durch die Brennweite f abgeschätzt. Diese Näherung ist gültig, solange der Objektivauszug vernachlässigt werden kann - also für alle Aufnahmen außerhalb des Makrobereiches. Zur Anschauung der einzelnen Größen sei wieder auf das Bild 1 verwiesen.
1.5 Sonderfall. Gerade bei
Aufnahmen mit sehr großer Stereobasis ist der Horizont
häufig in der Aufnahme enthalten. Daraus folgt für
den Fernpunkt der Sonderfall 
.
Für diesen Fall gilt die vereinfachte Beziehung:
. (3)
Alle Werte sind in Millimeter anzugeben. Beispiel: b0 = aN / 50 bei f = 50mm, b0 = aN / 100 bei f = 100mm u.s.w. Zwei Sachverhalte sind nun erkennbar:
-
Die weitverbreitete Faustformel b0 = aN / 50 gilt nur für die Standardbrennweite f = 50mm. Für Teleobjektive muß die Basis reduziert werden.
-
Bei endlicher Fernpunktweite wird die zulässige Stereobasis größer. Die Merkregel I ist dann nicht mehr gültig und die Basis sollte nun direkt mit (2) oder aber mit Hilfe der Rechenscheibe ermittelt werden.
Die Schwierigkeiten bei Aufnahmen mit vergrößerter Basis liegen eigentlich nicht so sehr in der mathematischen Berechnung des erforderlichen Basiswertes, sondern vielmehr in der Abschätzung der Entfernungen aN und aF. Beispiel: Man steht auf einem Berg und möchte ins Tal fotografieren. Wer kann schon sagen, ob der Nahpunkt 100m oder 200m entfernt ist? Will man ganz sicher gehen, sollte man in diesem Fall mehrere Aufnahmen mit unterschiedlicher Basis machen.
2. Aufnahmen mit verkleinerter Stereobasis
2.1 Technik. Für Makroaufnahmen in Stereo braucht man eine sehr viel kleinere Basis als den Augenabstand. Stilleben sind auch hier leicht mit einer Monokamera fotografierbar, bewegte Objekte dagegen nur mit Spezialausrüstungen, die man entweder selbst bauen muß (bekannt sind u.a. Geräte von Pat Whitehouse (GB), A.A. Pennings (NL), Fritz Ochotta (D), Fritz Bur am Orde (D) oder dem Autor), die nur noch selten bei antiquarischen Versteigerungen zu erstehen sind (z.B. Realist Macro Stereo Camera oder Nikonos mit MarinSolar) oder die man seit kurzer Zeit auch von der Firma RBT in Form eines Makrovorsatzgerätes für Spiegelreflex-Stereokameras erwerben kann.
Für den `Stereo-Normalverbraucher' heißt das zumeist, daß er sich auf Stilleben beschränken muß. Notwendig ist dazu lediglich eine Spiegelreflexkamera mit Makroeinrichtung, die zwischen den beiden Aufnahmen lediglich parallel (wichtig!) verschoben werden muss. Zusätzlich zu allen bekannten Problemen der Makrofotografie (etwa die geringe Tiefenschärfe) hat man auch hier wieder mit der Schwierigkeit zu kämpfen, daß geringste Veränderungen zwischen den beiden Aufnahmen den Stereoeindruck sofort erheblich stören. Die Verwendung eines Ringblitzgerätes ist z.B. völlig ausgeschlossen, da dieses am Objektiv befestigt wird und sich somit relativ zum Aufnahmeobjekt bewegt. Eine natürliche Beleuchtung ist nur möglich, wenn sie indirekt und sehr diffus auf das Objekt einstrahlt. Alle Reflexe sind richtungsabhängig und stark störend.
An den mechanischen Aufbau werden bezüglich der Stabilität erhöhte Anforderungen gestellt, sonst führt die Verschiebung der Kamera zu einem veränderten Ausschnitt (Rotationsfehler) oder zu einer veränderten Schärfenebene.
2.2 Gigantismus. Die Folge der verkleinerten Aufnahmebasis ist eine perspektivische Vergrößerung aller abgebildeten Gegenstände. Diesen Effekt nennt man Gigantismus. er wird - anders als der Liliputismus - selten als störend empfunden. Im Gegenteil, gelungene Aufnahmen sind sehr beeindruckend, worin ein besonderer Reiz der Stereomakrofotografie liegt.
2.3 Aufnahmegeometrie. Genauso wie bei den Aufnahmen mit vergrößerter Basis gilt hier ganz besonders die Forderung nach parallelen Aufnahmeachsen. Die nicht unübliche Methode, die Achsen bei der Aufnahme etwas nach innen zu neigen (konvergente Aufnahmeachsen) führt leider zu trapezförmigen Verzeichnungen, die sich nachträglich nicht mehr korrigieren lassen.
2.4 Berechnung der Aufnahmebasis. Einfache Formeln zur Basisberechnung, die auch schnell und unkompliziert handhabbar sind, fehlten bisher. Eine Umformung von Gleichung (1) liefert (keine Näherung):
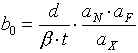. (4)
Hier ist ergänzend: ß: Vergrößerungsfaktor mit ß = a' /aX , t: Stereotiefe mit t = aF - aN und aX: Abstand Hauptebene zur Schärfenebene.
Die Stereo-Rechenscheibe für 'Nahaufnahmen' verwendet für diesen Fall die im Makrobereich sehr gute Näherung (siehe Anhang):
. (5)
. (6)
Diese Beziehung gewährleistet zum Selbstausrechnen oder im Zusammenhang mit der Rechenscheibe wiederum eine schnelle und unkomplizierte Ermittlung der gewünschten Basis.
2.5 Sonderfall. Sicherlich sind
nicht alle Kombinationen von ß und t
sinnvoll, denn große Objekte verlangen einen kleineren
Vergrößerungsfaktor und kleine Objekte einen
größeren. Die Erfahrung zeigt, daß ein
typischer Zusammenhang für das Produkt 
mit 
Bildbreite (
25 mm für
Kleinbild) gegeben ist. Dieser Ansatz setzt die
Objektgröße mit der Objekttiefe in
eine gewisse Abhängigkeit. Zunächst mag dies etwas
willkürlich erscheinen, in der Praxis ist dieser
Zusammenhang aber fast immer gegeben (Ausnahme: sehr tiefe
und sehr flache Objekte). Setzt man für die Deviation
wieder den Wert d = 1,2 mm ein, erhält man unter
Verwendung von (6) für Standardaufnahmesituationen die
einfache Merkregel II für Nahaufnahmen:
Dies gilt unabhängig von der Brennweite. Der Abstand aX muss von der Hauptebene des Objektivs gemessen werden. Die Lage der Hauptebene kann durch Ausmessen - zweckmäßigerweise in der Einstellung für ß = 1,0 - verhältnismäßig einfach ermittelt werden. Bei vielen Objektiven liegt sie etwa in der Ebene des Blendenringes.
Bemerkung zur Anwendung beider Regeln: Aufnahmen entsprechend den Vorschriften (3) und (6) besitzen immer die gleiche Deviation und bei richtiger Wahl dieser Deviation immer eine angenehme Tiefenwirkung. Dafür werden Objekte mit relativ großer Stereotiefe im Stereobild etwas gestaucht und Objekte mit sehr kleiner Stereotiefe etwas gestreckt. Die vereinfachte Merkregel II unterstellt zur Aufnahme immer ein Standardobjekt. Bei Objekten mit sehr großer Stereotiefe besteht also die Gefahr des Bildzerfalls, bei sehr kleiner Stereotiefe entstehen Flachbilder. Tip für die Praxis: Verwenden Sie immer zunächst die Merkregeln und experimentieren Sie selbst ein wenig mit der Stereobasis (bei flachen Objekten etwas mehr, bei tiefen Objekten etwas weniger Stereobasis nehmen).
2.6 Konvergente Aufnahmeachsen. Beim Parallelverschieben der gesamten Aufnahmevorrichtung besitzen beide Stereobilder etwas unterschiedlichen Bildinhalt. Das Aufnahmeformat kann dann nicht mehr ganz ausgenutzt werden, was besonders bei großen Vergrößerungsfaktoren sehr störend sein kann. Um das zu vermeiden, gibt es grundsätzlich zwei verschiedene Möglichkeiten:
-
Die Aufnahmeachsen verlaufen nicht mehr wie in Bild 1 gefordert parallel, sondern konvergieren im Aufnahmeobjekt. Wie schon unter 2.3 erwähnt, führt dies zu nicht mehr korrigierbaren Verzerrungen! So wird beispielsweise das Bild eines Rechtecks bei konvergenten Achsen zum Trapez, wie es in Bild 2 gezeigt wird. Da das längere Betrachten trapezverzerrter Stereoaufnahmen zu Kopfschmerzen führt, muss von dieser Methode unbedingt abgeraten werden!
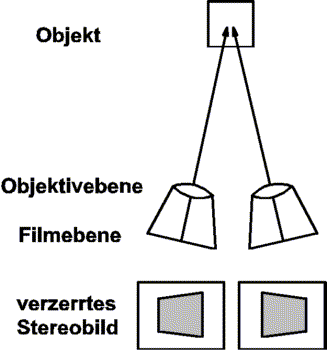
Bild 2: Trapezverzerrungen bei konvergierenden Aufnahmeachsen.
-
Einfacher handzuhaben und schneller zu guten Ergebnissen führt die Verwendung eines Balgengerätes mit verschiebbarer Objektiv- und Kamerastandarte (z.B. HAMA Shift). Die gewünschte Basis wird dann an der Objektivstandarte eingestellt und die Kamerastandarte jeweils so ausgerichtet, daß der Bildinhalt für beide Teilbilder identisch ist. Bild 3 demonstriert dieses Aufnahmeprinzip.
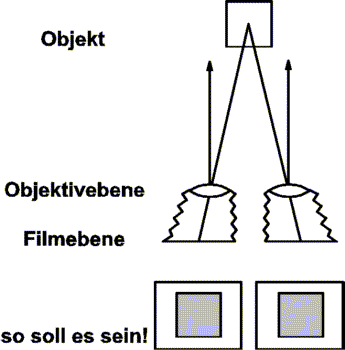
Bild 3: Parallele Aufnahmeachsen mit Scheinfensterkorrektur.
-
3. Noch ein Tipp zum Schluss
Die genaue Kenntnis der Deviation
läßt natürlich noch keine präzise
Aussage über die zu erwartende Raumwirkung zu, deshalb
ist es empfehlenswert, in kritischen Fällen mehrere
Aufnahmen zu machen. Eine effiziente Methode sei hier
vorgestellt: Zunächst ermittelt man einen Richtwert
für die Stereobasis b0 (nach Formel
oder Rechenscheibe) und macht anschließend vier
Aufnahmen, wobei ausgehend von der ersten Aufnahme
zunächst um b0 / 3, dann um
b0 und schließlich um 2
b0 / 3 weitergeschoben wird - so wie es in
Bild 4 skizziert ist. Auf diese Weise lassen sich
entsprechend Tabelle 1 sechs verschiedene
Stereo-Bildpaare mit unterschiedlicher Basis kombinieren.
 |
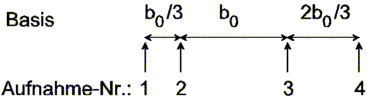| Bild 4: Aufnahmereihenfolge mit Basisberechnung. |
Damit bleibt dem Stereofotografen trotz aller Theorie immer noch die Möglichkeit, unter mehreren Teilbildkombinationen das nach seinem Geschmack beste Stereobildpaar auszuwählen.
|
||||||||||||||||||||||||||||
| Tabelle 1: Teilbildkombinationen mit resultierender Stereobasis. |
4. Anhang: Die Schärfenebene
Um im gegebenem Nahpunkt aN und Fernpunkt aF eine genau gleiche Unschärfe zu erhalten, muss der Objektivauszug so gewählt werden, dass sich die optimale Schärfe im Abstand aX ergibt:
. (7)
Für die Praxis ist Gleichung (7) etwas unhandlich, so dass häufig mit Näherungen gerechnet wird. Sehr weit verbreitet ist beispielsweise im Makrobereich die Näherung durch das arithmetische Mittel
, (8)
das den exakten Wert recht gut annähert, so lange aN und aF nicht allzu unterschiedlich sind. Für die Vereinfachung von Gleichung (4) ist weder (7) noch (8) geeignet. Es wird deshalb eine andere Näherung, das geometrische Mittel
(9)
verwendet, das übrigens die exakte Formel (7) im interessierenden Bereich auch wesentlich besser approximiert als das arithmetische Mittel.
[1] Fritz G. Waack: Stereofotografie, Selbstverlag Berlin, 4.Auflage 1985.
Dieser Artikel steht im Downloadbereich auch zum Herunterladen als pdf-Dokument bereit.
