Zur Wahl der richtigen Stereobasis
Gerhard P. Herbig, gph@herbig-3d.deZusammenfassung: Dieser Artikel gibt eine Übersicht über die verschiedenen Denkansätze zur Wahl einer geeigneten Stereobasis und deren jeweiligen Ergebnisse.
1. Fragestellung
Eine zentrale Frage, die sich bei der Stereofotografie immer wieder stellt, lautet:
Wie ist bei den unterschiedlichen Aufnahmesituationen (Fernaufnahmen / Normalaufnahmen / Makroaufnahmen) die jeweils passende Stereobasis zu wählen?
Welche Aufnahmen kann ich mit einer bestimmten gegebenen Stereobasis machen?
Um der Antwort auf diese beiden Fragen näher zukommen, gibt es zwei völlig verschieden Ansätze:
Methode 1: Wie ist die Stereobasis zu wählen, um bei der Diaprojektion einen möglichst naturgetreuen Bildeindruck zu erhalten (keine Deformationen, eine Kugel soll als Kugel und nicht als Ei wahrgenommen werden)?
Methode 2: Wie ist die Stereobasis zu wählen, um die gesamte Szenerie als ein einziges Raumbild ohne Bildzerfall wahrzunehmen?
Beide Ansätze sind im Prinzip sinnvoll und führen durch Anwendung geometrischer Methoden zu eindeutigen - aber eben unterschiedlichen - Ergebnissen!
Bei Methode 1 gehen in die Rechnung neben den Aufnahmebedingungen (Aufnahmebrennweite) auch die Wiedergabebedingungen ein, d.h., das Ergebnis ist auch vom Vergrößerungsfaktor der Projektion und vom Abstand des Betrachters zur Leinwand abhängig! Tatsächlich gibt es immer nur einen einzigen Punkt im Zuschauerraum, von dem aus das projizierte Stereobild verzerrungsfrei betrachtet werden kann, den sogenannten orthostereoskopischen Punkt (für eine tautostereoskopische Abbildung verlangt man neben der Verzerrungsfreiheit auch die Originalgröße des virtuellen Raumbildes). Aus diesem Grund ist die Berechnung der Stereobasis nach der Methode 1 eher akademischer Natur und wird in der Praxis auch seltener angewendet. Wen die Zusammenhänge trotzdem interessieren, kann im Artikel Tiefenwahrnehmung bei der Stereoprojektion die Herleitung der Bedingungen zur formtreuen Stereoprojektion nachvollziehen. Kapitel 2 gibt eine kurze Zusammenfassung der wichtigsten Ergebnisse.
Da Tiefenverzerrungen bei der Diaprojektion ohnehin nur festgestellt werden können, wenn dem Zuschauer gut bekannte Vergleichsobjekte (beispielsweise Menschen) gezeigt werden, ist die Berechnung der Stereobasis nach Methode 2, die lediglich eine obere Grenze für die in einem Stereobild enthaltene Tiefe verlangt, von größerer praktischer Bedeutung. Diese Methode stellt weiterhin sicher, dass die Ergebnisse ohne Augenschmerzen betrachtbar bleiben. Die Merkregeln aus Kapitel 4 basieren deshalb ausschließlich auf dieser Methode 2, deren wichtigsten Überlegungen in Kapitel 3 erläutert werden.
2. Die formtreue Stereoprojektion
Eine formtreue Stereoprojektion (orthostereoskopische Projektion) ist im strengen Sinne nur dann möglich, wenn die beiden korrespondierenden Unendlichpunkte im Augenabstand auf die Leinwand projiziert werden. Diesen Fall nennt man auch divergenzfreie oder natürliche Projektion.
Für diesen Fall ist das Raumbild genau dann formtreu, wenn (unabhängig von der verwendeten Stereobasis) der Betrachtungsabstand von der Leinwand aB gleich der V-fachen Aufnahmebrennweite fK ist (V ist die Projektionsvergrößerung):
Siehe dazu auch Gleichung (4.3) aus Tiefenwahrnehmung bei der Stereoprojektion. Die Größe des Objektes erscheint uns hierbei skaliert mit dem Faktor b0 / bK, also mit dem Verhältnis von Augenbasis b0 und Aufnahmebasis bK .
Räumlich begrenzte Objekte (die also den Unendlichpunkt nicht enthalten) erlauben bei der Rahmung und der Projektion größere Freiheiten, ohne dass gleich das Divergenzverbot verletzt würde. Streng genommen schließt der Fall der nicht-natürlichen Projektion (Unendlichpunkte z.B. in größerem als im Augenabstand auf der Leinwand, unanbhängig davon ob sichtbar oder nicht sichtbar) eine formtreue Projektion aus, jedoch erscheinen Objekte, die im Abstand
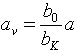
wahrgenommen werden, immer noch fast formtreu (quasi-orthostereoskopisch), siehe dazu Gleichung (5.9/3) aus Tiefenwahrnehmung bei der Stereoprojektion. (a ist der Abstand des Objektes bei der Aufnahme und av der virtuelle Abstand bei der Stereoprojektion). Immerhin ergibt sich hier ein gewisser Anhaltspunkt zur Wahl der Stereobasis: Wird beispielsweise verlangt, dass Objekte, die bei der Projektion in 3m Entfernung wahrgenommen werden, auch (fast) formtreu sein sollen, wäre als Aufnahmebasis
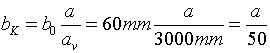 ,
,
also "Abstand/50" zu wählen. Tatsächlich wird in der Praxis aber häufig ein etwas größerer Wert bevorzugt.
3. Wann passiert Bildzerfall?
Stereosehen ist eine Leistung unsres Gehirns, das in der Lage ist, das linke und das rechte Stereo-Halbbild zu einem einzigen Raumbild zu fusionieren. Dieser Fusionsprozess wird immer dann gestört, wenn die beiden Stereo-Halbbilder zu große Unterschiede beziehungsweise das Raumbild eine zu große Tiefe aufweisen - man spricht dann von einem Bildzerfall. Man benötigt also ein Maß für die in einem Stereobild enthaltene Tiefe und wählt dafür die Differenz der parallaktischen Verschiebungen der Nahbild- und der Fernbildpunkte. Dieser Wert wird auch Deviation genannt (Beispiel dazu siehe unten).
Für die Diaprojektion hat es sich als günstig erwiesen, die Deviation nicht größer als 1/30 der Bildbreite zu wählen, also bei 36mm Bildbreite (Kleinbildformat) 1,2 mm und bei 60mm Bildbreite (Mittelformat) 2mm. Für das sogenannte amerikanische Format mit 24mm Bildbreite erhält man eine maximale Deviation von 0,8mm. Obwohl sich diese Grenzwerte mit einigen Annahmen von der sogenannten 70 Minuten-Bedingung ableiten lassen (siehe 70 Minuten-Bedingung und ihre Folgen) und diese 70 Minuten-Bedingung als sehr umstritten gilt, hat sich der obere Grenzwert Bildbreite/30 für die maximale Deviation, die ein Stereobild besitzen darf, in der Praxis seit Jahrzehnten bewährt! Für das Betrachten von gedruckten Stereobildern gelten übrigens höhere Grenzwerte, da hierbei die effektiven Betrachtungswinkel in der Regel kleiner sind.
4. Die Merkregeln
Ausgehend von dem Grenzwert für die Deviation (Bildbreite/30) kann die Stereobasis leicht berechnet werden (siehe Gleichung (3) aus Anmerkungen zur Stereofotografie mit verkleinerter oder vergrößerter Basis). Für die Bereiche der Normal- und Fernaufnahmen gilt die Merkregel I
Stereo-Basis < Nahpunktweite geteilt durch Brennweite
(alle Größen in Millimeter angeben), wobei die Nahpunktweite die Entfernung zum nächsten auf dem Bild sichtbaren Gegenstand ist.
Bei Makroaufnahmen, gilt dagegen die Merkregel II (Gleichung (6) im oben genannten Artikel):
Stereo-Basis < Abstand Objektiv-Objekt geteilt durch 20
Wichtig ist hier, den Abstand nur bis zum Objektiv (Hauptebene, in der Praxis ist das die Ebene des Blendenringes) und nicht bis zur Filmebene zu messen. Einzelheiten zur Ableitung dieser beiden Merkregeln finden sich im Artikel: Anmerkungen zur Stereofotografie mit variabler Basis.
Der obere Grenzwert "Abstand/20", der nicht überschritten werden sollte, ist also deutlich größer als der im obigen Beispiel errechnete Wert "Abstand/50". In der Praxis empfiehlt es sich deshalb immer, mehrerer Aufnahmen mit verschiedenen Basiswerten herzustellen und das für den jeweiligen Verwendungszweck Passende auszusuchen. (Tipp unter Freunden: Eher an "Abstand/20" orientieren als an "Abstand/50".)
Anhang: Die Deviation
Die Unterschiede im linken und rechten Halbbild eines korrekten Stereobildes bestehen ausschließlich aus dem seitlichen Versatz zweier korrespondierenden Bildpunkte. Alle anderen Unterschiede sind Bildfehler und sollten vermieden werden, da der Betrachtungsgenuss sonst empfindlich gestört werden kann.
Je größer dieser seitliche Versatz eines Bildpunktpaares ist, desto stärker ist der Raumeindruck. Sind dagegen linkes und rechtes Halbbild identisch, ist der Versatz für alle Bildpunktpaare gleich Null und das Bild erscheint flach. Die Differenz aus maximalem und minimalem Versatz, die in einem Stereobild vorkommen, nennt man Deviation (zuweilen auch maximale Querdisparation). Die Deviation ist eine Eigenschaft eines Stereobildes, messbar in üblichen Längeneinheiten. Die Angabe der Deviation in Absolutwerten macht allerdings nur Sinn, wenn auch die Abmessungen des ganzen Bildes bekannt sind. Besser ist es also, die Deviation gleich auf die Bildbreite zu beziehen, um einen Wert zu erhalten, der einen direkten Rückschluss auf die Tiefenwirkung des Stereobildes zulässt. Dieser Wert bleibt dann immer gleich, auch wenn man das Stereobild vergrößert oder verkleinert. Bei der Stereoprojektion sollte die obere Grenze "1/30" für diese normierte Deviation nicht überschritten werden.
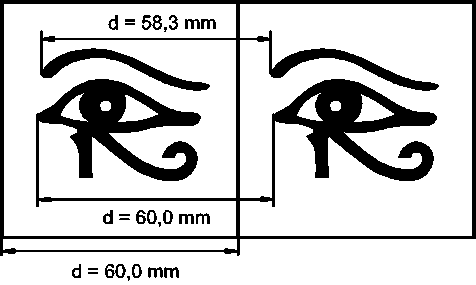
Beispiel: In diesem Bild beträgt der Versatz des Fernpunktes 60,0mm und der Versatz des Nahpunktes 58,3mm. Für die Deviation ergibt sich daraus:
d = 60,0mm - 58,3mm = 1,7mm. Die Bildgröße ist ebenfalls 60mm und deshalb die normierte Deviation = 1,7/60 = 0,0283. Dieser Wert ist kleiner als 1/30 (=0,0333) und deshalb ist die oben formulierte Forderung erfüllt.
Dieser Artikel steht im Downloadbereich auch zum Herunterladen als pdf-Dokument bereit.